
USACO 2024 December Contest, Bronze
Problem 2. Farmer John's Cheese Block
Contest has ended.

Log in to allow submissions in analysis mode
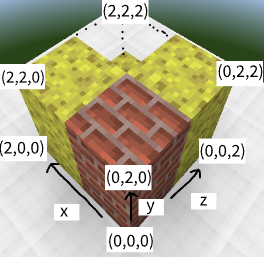
Farmer John has a block of cheese in the shape of a cube. It lies on the 3-dimensional coordinate plane, extending from $(0,0,0)$ to $(N, N, N)$ ($2 \leq N \leq 1000$). Farmer John will perform a series of $Q$ ($1 \leq Q \leq 2 \cdot 10^5$) update operations to his cheese block.
For each update operation, FJ will carve out the $1$ by $1$ by $1$ block of cheese extending from integer coordinates $(x, y, z)$ to $(x+1, y+1, z+1)$, where $0\le x,y,z<N$. It is guaranteed that there will exist a $1$ by $1$ by $1$ block of cheese at the location FJ carves. Since FJ is playing Moocraft, gravity does not cause parts of the cheese to fall if cheese below is carved.
After each update, output the number of distinct configurations that FJ can stick a $1$ by $1$ by $N$ brick in the cheese block such that no part of the brick overlaps with any remaining cheese. Every vertex of the brick must have integer coordinates in the range $[0,N]$ for all three axes. FJ may rotate the brick however he wants.
INPUT FORMAT (input arrives from the terminal / stdin):
The first line contains $N$ and $Q$.
The following $Q$ lines contain $x$, $y$, and $z$, the coordinates to be carved.
OUTPUT FORMAT (print output to the terminal / stdout):
After each update operation, output an integer, the number of configurations.
SAMPLE INPUT:
2 5 0 0 0 1 1 1 0 1 0 1 0 0 1 1 0
SAMPLE OUTPUT:
0 0 1 2 5After the first three updates, the $1\times 2 \times 1$ brick spanning $[0, 1]\times [0, 2]\times [0, 1]$ does not overlap with the remaining cheese, so it contributes toward the answer.
SCORING:
- Inputs 2-4: $N\le 10$ and $Q \le 1000$
- Inputs 5-7: $N\le 100$ and $Q \le 1000$
- Inputs 8-16: No additional constraints
Problem credits: Chongtian Ma, Alex Liang