The goal of this problem is to minimize a function $f(y)$ describing the total cost of manure transport if the teleporter endpoint is located at position $y$. Since $f(y)$ has a piecewise linear structure, we do this by scaning $y$ forward and tracing out $f(y)$, pausing at each breakpoint to adjust the current slope of $f(y)$ in an appropriate way, and maintaining a running minimum as we go. There are only $O(N)$ breakpoints so after sorting them in $O(N \log N)$ time we can scan through and trace out $f(y)$ in just $O(N)$ time.

Although the high-level algorithmic picture above is relatively straightforward, it takes a bit of mathematical effort to figure out where all the breakpoints in $f(y)$ need to go -- that is, at which value of $y$, and how much the slope changes at each breakpoint. Note that the total transport distance $f(y)$ can be broken down into the transport distance for each pile $i$,

$f(y) = \sum_{i=1}^N f_i(y)$,

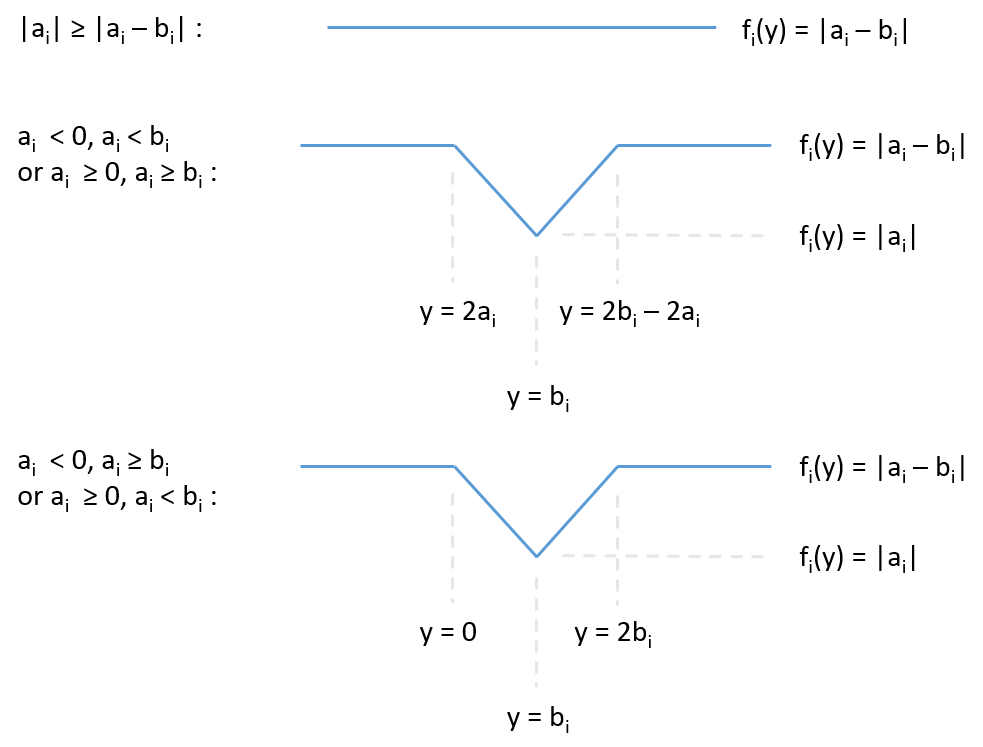
where $f_i(y) = \min(|a_i - b_i|, |a_i - 0| + |b_i - y|)$ represents the cost incurred only for transporting pile $i$ (the first part represents the transportation cost if moved directly, and the second part if teleported). Each of the $f_i$'s are reasonably simple functions of $y$. After a bit of mathematical wrangling, we can deduce that the $f_i$'s have the following shapes:

In terms of breakpoints these functions contribute to $f(y)$, for example if $|a_i| \geq |a_i - b_i|$, then there are no breakpoints in $f_i(y)$ at all -- the entire contribution of $f_i(y)$ is to shift $f(y)$ up by $|a_i - b_i|$. In another example case, if $a_i < 0$ and $a_i \geq b_i$, then $f_i$ has three breakpoints which contribute to $f(y)$: at $y = 0$ the slope of $f_i(y)$ (and hence also of $f$) decreases by 1, at $y = b$ it increases by +2, and at $y = 2b$ it decreases by 1.

My code below uses a map to store the slope changes at all the different breakpoints of $f$, after which it scans across these in sorted order of $y$ and simply traces out $f(y)$, keeping track of the minimum value it attains.

#include <iostream>
#include <fstream>
#include <map>
#include <algorithm>
using namespace std;
     
int N;
map<int,int> slopechg;   // slopechg[t] is how much the slope of f(y) changes when y=t
     
int main(void)
{
   ifstream fin ("teleport.in");
   ofstream fout ("teleport.out");

   long long current_f = 0, slope_f = 0, current_y = -2000000000;

   fin >> N;
   for (int i=0; i<N; i++) {
      int a, b;
      fin >> a >> b;
      current_f += abs(a-b);
      
      // Now add any slope change breakpoints...      
      if (abs(a) > abs(a-b)) continue;
      slopechg[b]+=2;
      if (a<b && a<0)   { slopechg[0]--; slopechg[2*b]--; }
      if (a<b && a>=0)  { slopechg[2*b-2*a]--; slopechg[2*a]--; }
      if (a>=b && a<0)  { slopechg[2*b-2*a]--; slopechg[2*a]--; }
      if (a>=b && a>=0) { slopechg[0]--; slopechg[2*b]--; }
   }      

   // Now scan y forward and apply slope changes to trace out f(y), keeping track of min
   long long min_f = current_f;
   for (auto p : slopechg) {
      int new_y = p.first, delta_slope = p.second;
      current_f += slope_f * (new_y - current_y);
      current_y = new_y;
      slope_f += delta_slope;
      min_f = min(min_f, current_f);
   }

   fout << min_f << "\n";
   return 0;
}