Processing math: 100%
(Analysis by Suhas Nagar)

Claim 1: Bessie's path will consist of up to three segments: some walk along the X-axis, some walk from a point on the X-axis to a point on the Y-axis and some walk along the Y-axis. Any alternative path can be shown to be transformed into an equal or shorter distance path via the triangle inequality. This also means that Bessie's path will always be of the form a+√b which means that we can easily compute ⌊a+√b⌋=a+⌊√b⌋.

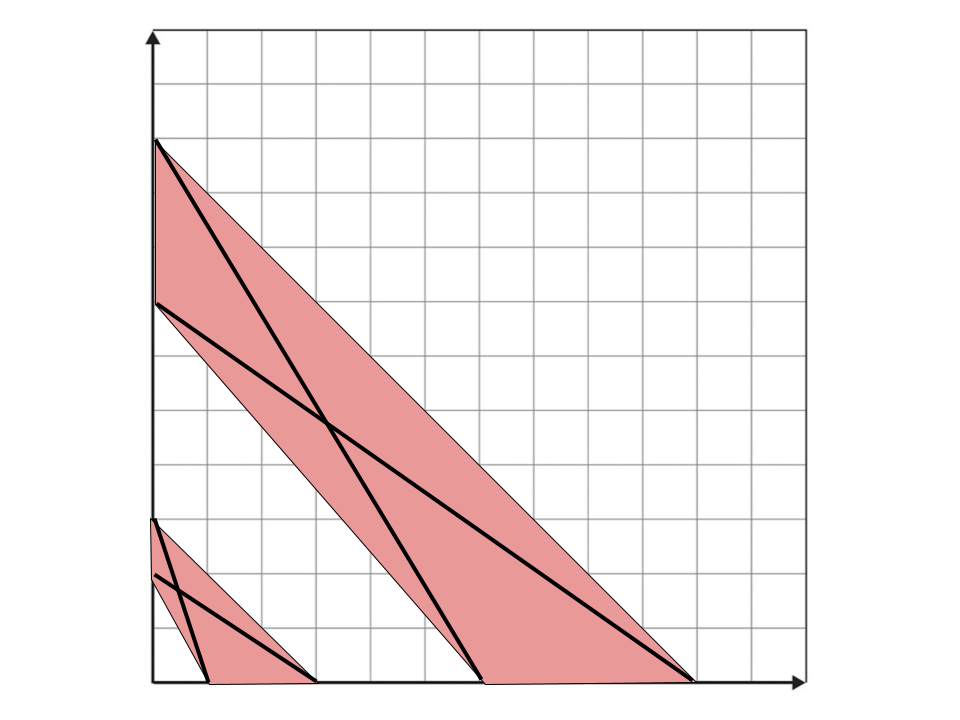
Let a photo op from x to y be denoted by x−y. We notice that two lines x1−y1 and x2−y2 cross where x1<x2 and y2<y1. If this is the case, it is impossible for Bessie to cross from x to y where x≤x2 and y≥y2 or x≥x1 and y≤y1 as she will always intersect one of these lines. This leads us to the observation that the photo ops segment the XY-plane into "good" regions and "bad" regions (indicated by the red in the image below) where Bessie can only cross within a "good" region where a region can be defined by its endpoints x1,y1,x2,y2 where x1<x2 and y1<y2.

Suppose that we know the list of "good" regions at some time i. To compute the best estimate di for time i, we want to determine the best estimate for a path that goes through a given region, for every region.

We can define the function clip(p,[a,b]) as follows: If p is within the interval [a,b], then it maps to itself, otherwise it maps to the closest point in the interval.

Observation: For a specific "good" region x1,y1,x2,y2, there aren't many cases to consider for the best path. The optimal path from X to Y must pass through both clip(X,[x1,x2]) and clip(Y,[y1,y2]). Since the region is "good", we know that Bessie can make her path X→clip(X,[x1,x2])→clip(Y,[y1,y2])→Y without crossing any lines.

Subtask 2:

The important part of the previous observation is that the only "important" points to consider are endpoints of the photo ops, X, and Y. We can utilize this simplification to solve the second subtask. For every important x, we can maintain the smallest and largest y-coordinate it can directly reach (meaning y-coordinates included in the “good” regions to the left and right of x). We iterate over all the lines in the time order and record how the lines bound the reachable y-coordinates.

We can take minimum across all x to get the best estimates for every time. Since we iterate over all N+1 important x points, and we iterate over all N lines for every coordinate, so the time complexity of this solution would be O(N2).

Note that the following solution uses a sqrt_safe function to compute the square root of a number. Although coordinates were small enough, a square root function of this form ensures that precision issues don't cause correctness issues.

Spencer Compton's C++ Code: 

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pb push_back
 
int INF = (int)2e6;
int sqrt_safe(ll a, ll b){
    ll val = a*a+b*b;
    ll ret = (ll)sqrt(val)-1LL;
    while((ret+1LL)*(ret+1LL)<=val){
        ret++;
    }
    return ret;
}
int snap(int l, int r, int x){
    if(x < l){
        return l;
    }
    if(x > r){
        return r;
    }
    return x;
}
int calc(int cX, pair<int, int> yRange, int X, int Y){
    int cY = snap(yRange.first,yRange.second,Y);
    int ret = abs(cX-X)+abs(cY-Y)+sqrt_safe(cX,cY);
    return ret;
}
int main(){
    int N, T;
    int X, Y;
    cin >> N >> T >> X >> Y;
    vector<int> s, x, y;
    for(int i = 0; i<N; i++){
        int a, b, c;
        cin >> a >> b >> c;
        s.pb(a);
        x.pb(b);
        y.pb(c);
    }
    vector<int> ans(T,X+Y);
    x.pb(X);
 
    for(auto curX : x){
        int point = 0;
        int lo = 0;
        int hi = INF;
        for(int t = 0; t<T; t++){
            while(point<N && s[point]<=t){
                int tmpX = x[point];
                int tmpY = y[point];
                if(tmpX < curX){
                    lo = max(lo,tmpY);
                }
                else if(tmpX > curX){
                    hi = min(hi,tmpY);
                }
                point++;
            }
            if(lo<=hi){
                ans[t] = min(ans[t],calc(curX,make_pair(lo,hi),X,Y));
            }
            else{
                break;
            }
        }
    }
    
    for(int t = 0; t<T; t++){
        cout << ans[t] << "\n";
    }
}

Full Solution:

From earlier, we know that if we know all our "good" regions for a given time, the best estimate is simple to calculate for a specific region since there are very limited important points that Bessie can cross between in a single region. This motivates trying to find an efficient way to maintain our regions. Note that if we know the "bad" regions, we can easily determine the "good" regions to be the space in between "bad" regions, so maintaining either set of regions is equivalent.

Suppose that we already know our "bad" regions and we add a line. Since a line can be thought of as a "bad" region on its own with endpoints equivalent to the endpoints of the line, we just need to perform a merge of the "bad" region formed by this line with the other regions in our set. More specifically, if multiple regions intersect with our new bad region, we can delete these regions, merge them with the line into a single region R and add it to our set.

Every "bad" region can only be created once or merged into another region once, so we will only ever have O(regions)=O(N) operations to perform. We can associate a pair of consecutive "bad" regions with an estimate for how long it takes to travel in the "good" region between. Our answer would then just be picking the smallest estimate.

We just need to be careful about only maintaining estimates for regions that still exist by removing estimates for regions that get merged and adding the estimates for new regions that get added (we need to also make sure we consider the estimates for a given region with the region to its left and right).

Since the entire XY-plane is "good" at the beginning, we can start off with two "bad" regions in our set, where the first one has all of its endpoints at 0 and the second one has all of its endpoints at 1e9 (or some equivalent large value that will never be crossed). This allows our initial path to always pass through the "good" region between, which is effectively unconstrained.

We can use a multiset (or some equivalent data structure) to maintain our estimates, and ordered sets to maintain our "bad" regions, and all our updates can occur in O(NlogN) which gives us our full solution.

Benjamin Qi's C++ Code: 

#include <bits/stdc++.h>
using namespace std;

using ll = long long;
using pi = pair<int, int>;
using ppi = pair<pi, pi>;

ll sq(ll x) { return x * x; }

int sqrt_safe(ll x) {
    assert(x >= 0);
    int s = sqrt(x);
    while (!(sq(s + 1) > x)) ++s;
    while (sq(s) > x) --s;
    return s;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int N, T, X, Y;
    cin >> N >> T >> X >> Y;
    multiset<ppi> bad;
    multiset<ll> cands;

    auto make_range = [&](ll &ans, pi x_range, int &x) {
        assert(x_range.first <= x_range.second);
        if (x < x_range.first) {
            ans += x_range.first - x;
            x = x_range.first;
        }
        if (x > x_range.second) {
            ans += x - x_range.second;
            x = x_range.second;
        }
    };
    auto get_cost = [&](pair<pi, pi> l, pair<pi, pi> r) {
        pi x_range{l.first.second, r.first.first};
        pi y_range{l.second.second, r.second.first};
        int cx = X, cy = Y;
        ll ans = 0;
        make_range(ans, x_range, cx);
        make_range(ans, y_range, cy);
        ans += sqrt_safe(sq(cx) + sq(cy));
        return ans;
    };
    auto add_cost = [&](pair<pi, pi> l, pair<pi, pi> r, int sgn) {
        auto c = get_cost(l, r);
        if (sgn == 1) cands.insert(c);
        else {
            auto it = cands.find(c);
            assert(it != end(cands));
            cands.erase(it);
        }
    };
    auto isect = [&](ppi a, ppi b) {
        assert(a <= b);
        if (a.first.second <= b.first.first &&
            a.second.second <= b.second.first)
            return 0;
        return 1;
    };
    auto add = [&](auto it, int sgn) {
        bool has_prev = it != begin(bad);
        bool has_next = next(it) != end(bad);
        if (has_prev) add_cost(*prev(it), *it, sgn);
        if (has_next) add_cost(*it, *next(it), sgn);
        if (has_prev && has_next) add_cost(*prev(it), *next(it), -sgn);
    };
    auto merge_pair = [&](pi &a, pi b) {
        a.first = min(a.first, b.first);
        a.second = max(a.second, b.second);
    };
    auto merge_pairs = [&](ppi &a, ppi b) {
        merge_pair(a.first, b.first);
        merge_pair(a.second, b.second);
    };

    auto ins_line = [&](int x, int y) {
        ppi p{{x, x}, {y, y}};
        while (true) {
            auto it = bad.lower_bound(p);
            if (it != end(bad) && isect(p, *it)) {
                add(it, -1);
                merge_pairs(p, *it);
                bad.erase(it);
                continue;
            }
            if (it != begin(bad) && isect(*prev(it), p)) {
                auto IT = prev(it);
                add(IT, -1);
                merge_pairs(p, *IT);
                bad.erase(IT);
                continue;
            }
            break;
        }
        auto it = bad.insert(p);
        add(it, 1);
    };
    for (int x : {0, (int)1e9}) ins_line(x, x);
    vector<vector<pi>> upds(T);
    for (int i = 0; i < N; i++) {
        int s, x, y;
        cin >> s >> x >> y;
        upds.at(s).push_back({x, y});
    }
    for (int i = 0; i < T; i++) {
        for (auto [x, y] : upds.at(i)) ins_line(x, y);
        cout << *begin(cands) << '\n';
    }
}