
USACO 2022 February Contest, Platinum
Problem 1. Paint by Rectangles
Contest has ended.

Log in to allow submissions in analysis mode
Still being an avant-garde artist, Bessie decides that the painting should resemble a Holstein cow. More specifically, each region formed by the rectangles is colored either black or white, no two adjacent regions have the same color, and the region outside of all the rectangles is colored white.
After choosing the rectangles, Bessie would like you to output one of two things based on a parameter $T$:
- If $T=1$, output the total number of regions.
- If $T=2$, output the number of white regions followed by the number of black regions.
**Note: the time limit for this problem is 4s, twice the default.**
INPUT FORMAT (input arrives from the terminal / stdin):
The first line contains $N$ and $T$.The next $N$ lines each contain the description of a rectangle in the form $(x_1,y_1), (x_2,y_2)$ where $1\le x_1<x_2\le 2N$ and $1\le y_1<y_2\le 2N$. $(x_1, y_1)$ and $(x_2, y_2)$ are the bottom left and top right corners of the rectangle respectively.
It is guaranteed that all the $x_i$ form a permutation of $1\ldots 2N$, and the same holds for all the $y_i$.
OUTPUT FORMAT (print output to the terminal / stdout):
A single integer if $T=1$, otherwise two separated by spaces.SAMPLE INPUT:
2 1 1 1 3 3 2 2 4 4
SAMPLE OUTPUT:
4
There are two white regions and two black regions, for a total of four regions. The boundaries of all rectangles are connected, so this input would satisfy the conditions of subtask 3.

SAMPLE INPUT:
5 2 1 5 3 6 5 4 7 9 4 1 8 3 9 8 10 10 2 2 6 7
SAMPLE OUTPUT:
4 5
The boundary of the rectangle in the upper-right is not connected to the rest of the boundaries, so this input would not satisfy the conditions of subtask 4.
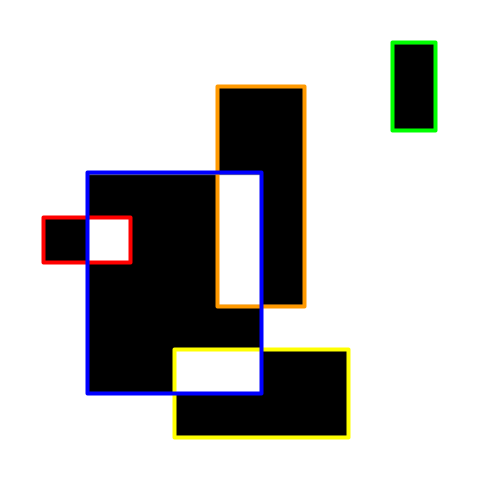
SCORING:
- Test cases 3-4 satisfy $N\le 10^3$.
- In test cases 5-7, no two rectangle boundaries intersect.
- In test cases 8-10, $T=1$ and the boundaries of all rectangles are connected.
- In test cases 11-13, $T=2$ and the boundaries of all rectangles are connected.
- In test cases 14-18, $T=1$.
- In test cases 19-23, $T=2$.
Problem credits: Andi Qu