
USACO 2020 US Open Contest, Gold
Problem 2. Favorite Colors
Contest has ended.

Log in to allow submissions in analysis mode
There exist $M$ pairs of cows $(a,b)$ such that cow $b$ admires cow $a$ ($1\le M\le 2\cdot 10^5$). It is possible that $a=b$, in which case a cow admires herself. For any color $c$, if cows $x$ and $y$ both admire a cow with favorite color $c$, then $x$ and $y$ share the same favorite color.
Given this information, determine an assignment of cows to favorite colors such that the number of distinct favorite colors among all cows is maximized. As there are multiple assignments that satisfy this property, output the lexicographically smallest one (meaning that you should take the assignment that minimizes the colors assigned to cows $1\ldots N$ in that order).
INPUT FORMAT (file fcolor.in):
The first line contains $N$ and $M$.The next $M$ lines each contain two space-separated integers $a$ and $b$ ($1\le a,b\le N$), denoting that cow $b$ admires cow $a$. The same pair may appear more than once in the input.
OUTPUT FORMAT (file fcolor.out):
For each $i$ in $1\ldots N$, output the color of cow $i$ in the desired assignment on a new line.SAMPLE INPUT:
9 12 1 2 4 2 5 8 4 6 6 9 2 9 8 7 8 3 7 1 9 4 3 5 3 4
SAMPLE OUTPUT:
1 2 3 1 1 2 3 2 3
In the image below, the circles with bolded borders represent the cows with
favorite color 1.
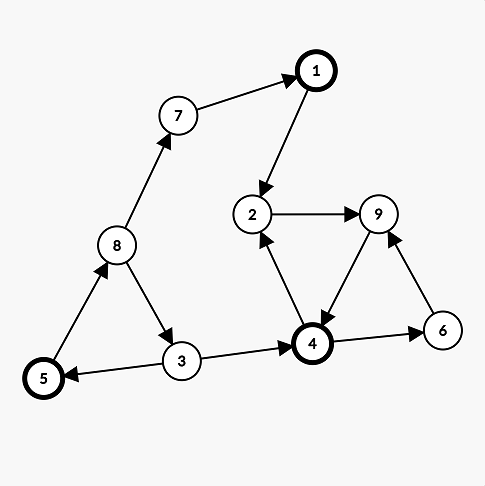
SCORING:
- Test cases 2-3 satisfy $N,M\le 10^3$.
- Test cases 4-10 satisfy no additional constraints.
Problem credits: William Lin and Benjamin Qi