Analysis: Taxi by Mark Gordon

This problem was solved in a couple different ways during the competition. This analysis will discuss a method of solving commonly used amongst competitors and then another solution based on min cost matching.

First, notice that Bessie never needs to drive a cow away from her destination. Therefore we drive a total distance of with a cow in the car. All that remains is computing how much driving we do without a cow in the car.

Consider any closed interval that contains no cow starting positions or ending positions. Considering position 0, where Bessie starts her travel, as an end position, we can compute a lower bound on the number of times that interval must be crossed without a cow. If there are more end positions than starting positions to the left of the interval than the interval must be crossed going right equal to the amount the end positions exceed the starting positions. This is because all starting positions must eventually be absorbed by an ending position. A similar argument holds when starting positions exceed ending positions for how many times we must go left.

To show the solution is also an upper bound on the answer note that Bessie has no need to turn around part way through an interval. The next thing to notice is the difference in the number of times an interval is crossed right and crossed left (including when she's moving cows) is always 1. Discounting the times she's moving cows in her car we get that the interval is crossed the same number of times, and in the same direction, as in our lower bound construction.

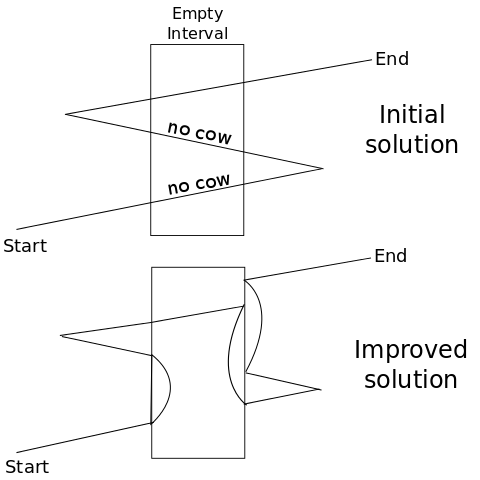
To close out the proof, note that Bessie should never cross an interval in both directions without a cow. This is why it was important that Bessie can drop off a cow anywhere. The below diagram shows how we can stitch together a path that crosses an empty interval twice without a cow. Notice that it's impossible for our changes to interrupt the solution as a whole if we stitch the paths back together the very first time Bessie crosses back to the right of the interval. We can do a similar construction in the other case when we cross to the right with the cow first.

Despite an involved analysis, the code ends up being pretty simple.

#define MAXN 100010

int A[MAXN];
int B[MAXN];

int main() {
  freopen("taxi.in", "r", stdin);
  freopen("taxi.out", "w", stdout);

  int N, M;
  cin >> N >> M;

  long long res = 0;
  vector<int> xs;

  vector<pair<int, int> > A;
  A.push_back(make_pair(0, 1));
  A.push_back(make_pair(M, -1));
  for(int i = 0; i < N; i++) {
    int s, e;
    cin >> s >> e;
    A.push_back(make_pair(s, -1));
    A.push_back(make_pair(e, 1));
    res += (int)abs(s - e);
  }
  sort(A.begin(), A.end());

  int psum = A[0].second;
  for(int i = 1; i < A.size(); i++) {
    res += 1ll * (A[i].first - A[i - 1].first) * (int)abs(psum);
    psum += A[i].second;
  }
  cout << res << '\n';
}

The min cost matching solution comes from the idea that we need to match each ending position with a starting position of the next cow. For this purpose it makes sense to consider there being an additional cow that wants to go from M to 0 that we deliver at the end for no cost. Excluding the driving cost when Bessie has a cow in the car, the cost of this matching clearly gives us a lower bound on the cost of delivering all the cows.

Unfortunately, the permutation of cows induced from the matching may not be a single cycle. However, we can stitch together any two overlapping cycles to create one larger cycle. Since all cycles overlap with the cycle containing the additional cow (going from M to 0) we conclude we can create a single cycle which forms a complete route. This route then, gives us a solution. Computing the min cost flow for this special case problem is done simply by sorting the starts and ends and matching things at the same index. Code for this solution is below.

#define MAXN 100010

int A[MAXN];
int B[MAXN];

int main() {
  freopen("taxi.in", "r", stdin);
  freopen("taxi.out", "w", stdout);

  int N, M;
  cin >> N >> M;

  long long res = 0;
  for(int i = 0; i < N; i++) {
    cin >> A[i] >> B[i];
    res += (int)abs(A[i] - B[i]);
  }
  A[N] = M;
  B[N] = 0;
  N++;

  sort(A, A + N);
  sort(B, B + N);
  for(int i = 0; i < N; i++) {
    res += (int)abs(A[i] - B[i]);
  }
  cout << res << '\n';
}