Subtask 1: $N$ is small.
We can view each grid cell as a node in a graph, where two neighboring cells are joined by an edge if there is no rectangle boundary between them.
Each connected component in this graph corresponds to a colored region in the painting. We can find these connected components in $\mathcal O(N^2)$ time using DSU. To find the colors of each region, we can create a new graph where each node is a connected component, and two nodes are joined by an edge if they touch each other in the painting.
The resulting graph will be bipartite, and we can run a DFS on it to get the colors.
Andi's code:
#include <iostream>
#include <numeric>
#include <utility>
#include <vector>
#include <queue>
#include <tuple>
using namespace std;
int n, t, cmp[2001 * 2001];
pair<int, int> vert[2001], horiz[2001];
vector<int> graph[2001 * 2001];
bool visited[2001 * 2001];
int find(int A) { return cmp[A] = A == cmp[A] ? A : find(cmp[A]); }
void onion(int A, int B) { cmp[find(A)] = find(B); }
int flat(int x, int y) { return x * (2 * n + 1) + y; }
bool inside(int x, int y) { return x >= 0 && x <= 2 * n && y >= 0 && y <= 2 * n; }
int main() {
cin.tie(0)->sync_with_stdio(0);
cin >> n >> t;
iota(cmp, cmp + (2 * n + 1) * (2 * n + 1), 0);
for (int i = 0; i < n; i++) {
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
vert[x1] = vert[x2] = {y1, y2 - 1};
horiz[y1] = horiz[y2] = {x1, x2 - 1};
}
for (int x = 0; x <= 2 * n; x++) {
for (int y = 0; y <= 2 * n; y++) {
if (inside(x + 1, y) && (y < vert[x + 1].first || y > vert[x + 1].second))
onion(flat(x, y), flat(x + 1, y));
if (inside(x - 1, y) && (y < vert[x].first || y > vert[x].second))
onion(flat(x, y), flat(x - 1, y));
if (inside(x, y + 1) && (x < horiz[y + 1].first || x > horiz[y + 1].second))
onion(flat(x, y), flat(x, y + 1));
if (inside(x, y - 1) && (x < horiz[y].first || x > horiz[y].second))
onion(flat(x, y), flat(x, y - 1));
}
}
for (int x = 0; x <= 2 * n; x++) {
for (int y = 0; y <= 2 * n; y++) {
if (inside(x + 1, y) && find(flat(x, y)) != find(flat(x + 1, y))) {
graph[find(flat(x, y))].push_back(find(flat(x + 1, y)));
graph[find(flat(x + 1, y))].push_back(find(flat(x, y)));
}
if (inside(x - 1, y) && find(flat(x, y)) != find(flat(x - 1, y))) {
graph[find(flat(x, y))].push_back(find(flat(x - 1, y)));
graph[find(flat(x - 1, y))].push_back(find(flat(x, y)));
}
if (inside(x, y + 1) && find(flat(x, y)) != find(flat(x, y + 1))) {
graph[find(flat(x, y))].push_back(find(flat(x, y + 1)));
graph[find(flat(x, y + 1))].push_back(find(flat(x, y)));
}
if (inside(x, y - 1) && find(flat(x, y)) != find(flat(x, y - 1))) {
graph[find(flat(x, y))].push_back(find(flat(x, y - 1)));
graph[find(flat(x, y - 1))].push_back(find(flat(x, y)));
}
}
}
queue<pair<int, bool>> q;
int black = 0, white = 0;
q.push({find(0), false});
visited[find(0)] = true;
while (q.size()) {
int curr, colour;
tie(curr, colour) = q.front();
if (colour) black++; else white++;
q.pop();
for (int i : graph[curr]) if (!visited[i]) {
visited[i] = true;
q.push({i, !colour});
}
}
if (t == 2) cout << white << ' ' << black << '\n';
else cout << white + black << '\n';
}
Subtask 2: No rectangle boundaries intersect.
Firstly, note that there will be exactly $N + 1$ colored regions, so we just have to find the color of each region.
The key observation for this subtask is that the color that a rectangle is immersed in is determined by the number of rectangles containing it. More specifically, if there is an even number of rectangles containing it, then it will be immersed in white; otherwise, it will be immersed in black. From this, we can find the color of each region.
The number of rectangles that contain rectangle $R$ is equal to how many more top edges than bottom edges there are that:
Intuitively, this is because rectangle $S$'s top and bottom edges "sandwich" rectangle $R$ (and by extension, $R$'s left edge) if and only if $S$ contains $R$.
We can then use a line sweep to find which color each rectangle is immersed in. First, we sort the rectangles' left and right edges by $x$-coordinate and process them in that order. Each time we encounter a left edge, we insert its rectangle's top and bottom edges into an "active" set, and we remove those edges when we encounter a right edge. We can then use a Fenwick tree (or whichever data structure you prefer for range sum queries) to count the edges we want in $\mathcal O(N \log N)$ time.
Ben's code (using an indexed set):
#include <bits/stdc++.h>
using namespace std;
#include <ext/pb_ds/assoc_container.hpp>
using namespace __gnu_pbds;
template<class T> using Tree = tree<T, null_type, less<T>,
rb_tree_tag, tree_order_statistics_node_update>;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int N, T; cin >> N >> T;
vector<pair<int,int>> ival(2*N+1);
for (int i = 0; i < N; ++i) {
int x1, y1, x2, y2; cin >> x1 >> y1 >> x2 >> y2;
ival[x1] = ival[x2] = {y1,y2};
}
Tree<int> active;
array<int,2> ans{1,0}; // white, black
for (int x = 1; x <= 2*N; ++x) {
auto [y1, y2] = ival[x];
if (active.find(y1) != active.end()) {
active.erase(y1), active.erase(y2);
} else {
active.insert(y1), active.insert(y2);
int color = active.order_of_key(y1);
color &= 1;
color ^= 1;
++ans[color];
}
}
if (T == 1) cout << ans[0]+ans[1];
else cout << ans[0] << " " << ans[1];
cout << "\n";
}
Subtasks 3: The rectangle boundaries are connected and $T = 1$.
We can treat the painting as a planar graph and use Euler's formula to solve this subtask. Euler's formula states that:
Where $F$ is the number of faces (i.e., the answer), $E$ is the number of edges, $V$ is the number of vertices, and $C$ is the number of connected components.
In this subtask, $C = 1$, so we only need to worry about finding $E$ and $V$.
If we treat each line segment in the painting as an edge and each corner/intersection as a node, then $V = 4N + (\text{# of intersections})$ because there are initially $4N$ rectangle corners. Similarly, $E = 4N + 2 \cdot (\text{# of intersections})$ because each intersection of rectangle edges results in $2$ additional line segments and there are initially $4N$ rectangle edges.
The answer is then $F = 2 + (\text{# of intersections})$. We can use a line sweep (for example, the algorithm described in this Topcoder article) to find the number of intersections in $\mathcal O(N \log N)$ time.
Ben's code:
#include <bits/stdc++.h>
using namespace std;
#include <ext/pb_ds/assoc_container.hpp>
using namespace __gnu_pbds;
template<class T> using Tree = tree<T, null_type, less<T>,
rb_tree_tag, tree_order_statistics_node_update>;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int N, T; cin >> N >> T;
assert(T == 1);
vector<pair<int,int>> ival(2*N+1);
for (int i = 0; i < N; ++i) {
int x1, y1, x2, y2; cin >> x1 >> y1 >> x2 >> y2;
ival[x1] = ival[x2] = {y1,y2};
}
Tree<int> active;
uint64_t ans = 2;
for (int x = 1; x <= 2*N; ++x) {
auto [y1, y2] = ival[x];
if (active.find(y1) != active.end()) {
active.erase(y1), active.erase(y2);
ans += active.order_of_key(y2)-active.order_of_key(y1);
} else {
ans += active.order_of_key(y2)-active.order_of_key(y1);
active.insert(y1), active.insert(y2);
}
}
cout << ans << "\n";
}
Subtasks 4: The rectangle boundaries are connected and $T = 2$.
Let's focus on finding the number of black regions.
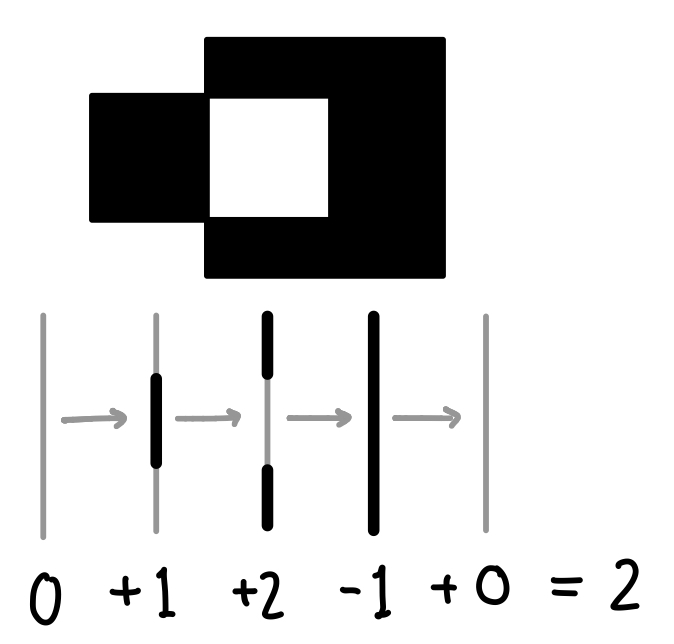
If we add rectangles to the plane sequentially, we can view each as inverting the colors on its inside. Using this analogy, we may imagine a white line sweeping through the plane from left to right, where each vertical edge that it encounters inverts the colors on an interval.
If we draw this out for a few small cases, we may notice there are three possible events:
We don't care about the first case because it doesn't change the number of black regions. The second case increments the number of black regions because it marks the start (i.e., leftmost edge) of a black region. The third case decrements the number of black regions because it means that we over-counted the number of black regions.
Below is an example of what this algorithm looks like:

We can then use a Fenwick tree (or whichever data structure you prefer for range sum queries) to count the number of each type of event in $\mathcal O(N \log N)$ time, and get our answer from that.
Ben's code:
#include <bits/stdc++.h>
using namespace std;
#include <ext/pb_ds/assoc_container.hpp>
using namespace __gnu_pbds;
template<class T> using Tree = tree<T, null_type, less<T>,
rb_tree_tag, tree_order_statistics_node_update>;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int N, T; cin >> N >> T;
vector<pair<int,int>> ival(2*N+1);
for (int i = 0; i < N; ++i) {
int x1, y1, x2, y2; cin >> x1 >> y1 >> x2 >> y2;
ival[x1] = ival[x2] = {y1,y2};
}
Tree<int> active;
uint64_t ans = 2, black = 0;
for (int x = 1; x <= 2*N; ++x) {
auto [y1, y2] = ival[x];
if (active.find(y1) != active.end()) {
int l = active.order_of_key(y1), r = active.order_of_key(y2);
ans += r-l-1;
black += (r+1)/2-(l+1)/2-1;
active.erase(y1), active.erase(y2);
} else {
active.insert(y1), active.insert(y2);
int l = active.order_of_key(y1), r = active.order_of_key(y2);
ans += r-l-1;
black += (r+1)/2-(l+1)/2;
}
}
if (T == 1) cout << ans;
else cout << ans-black << " " << black;
cout << "\n";
}
However, note that this algorithm only works when there is 1 connected component. The simplest case where this algorithm fails is the case where we have a single square contained in another square (i.e., a black donut). Our algorithm would return $0$ black regions, even though the answer is $1$.
Subtasks 5: $T = 1$.
The solution to this subtask is similar to that of subtask 3, but we need to find $C$ (the number of connected components).
We essentially need a structure that supports (in $\mathcal O(\log N)$ time):
To do this, we can use a segment tree.
One approach we might think of is to sweep a line from left to right while maintaining lists of points in each node's range. When we process a new rectangle, we can use DSU to merge its component with the component of each point in each relevant node, and then insert the top and bottom corners of the rectangle into the segment tree.
The problem with this approach is that we might do $\mathcal O(N^2)$ merges. However, many of those merges are redundant – if rectangles $A$, $B$ and $C$ all intersect, then we only need to do $2$ merges instead of the $3$ that we would've done.
To avoid this redundancy, we can store just $2$ values in each segment tree node:
While we are inserting a point with component $v$ into the segment tree and we encounter node $w$, then:
Subtasks 6: $T = 2$.
In addition to counting the connected components formed by the rectangles, we also need to count how many connected components are immersed in which color.
Why would these numbers help us? Recall the case where our subtask 4 solution fails. Since we have $1$ connected component immersed in black, we end up under-counting the number of black regions by $1$. In fact, one could prove that having $x$ connected components immersed in some color results in under-counting regions with that color by exactly $x$.
To solve this problem fully, we can implement the following algorithm:
Below is Daniel's C++ code for this problem:
#include <cassert>
#include <cstdio>
#include <map>
int N;
int ft[200005];
void update(int i, int v) {
for (; i <= N * 2; i += (i & -i)) {
ft[i] += v;
}
}
int query(int i) {
int ac = 0;
for (; i > 0; i -= (i & -i)) {
ac += ft[i];
}
return ac;
}
int uf[100005];
int find(int a) { return (a == uf[a]) ? a : (uf[a] = find(uf[a])); }
void merge(int a, int b) { uf[find(a)] = find(b); }
int st_lazy[800005]; // lazy merge with range, only nonzero if st_cnt is
// nonzero
int st_cnt[800005];
int who[200005]; // who[l]=who[r]=id
void apply(int w, int v) {
if (!st_cnt[w]) return;
if (st_lazy[w]) {
merge(v, st_lazy[w]);
} else {
st_lazy[w] = v;
}
}
void push(int w, int L, int R) {
if (st_lazy[w]) {
if (R - L > 1) {
apply(w * 2 + 1, st_lazy[w]);
apply(w * 2 + 2, st_lazy[w]);
} else {
merge(st_lazy[w], who[R]);
}
st_lazy[w] = 0;
}
}
void pull(int w, int L, int R) {
assert(R - L > 1);
st_cnt[w] = st_cnt[w * 2 + 1] + st_cnt[w * 2 + 2];
}
void update_range_merge(int w, int L, int R, int a, int b, int v) {
push(w, L, R);
if (a >= R || b <= L) return;
if (a <= L && b >= R) {
apply(w, v);
push(w, L, R);
} else {
int M = (L + R) / 2;
update_range_merge(w * 2 + 1, L, M, a, b, v);
update_range_merge(w * 2 + 2, M, R, a, b, v);
pull(w, L, R);
}
}
void update_inc(int w, int L, int R, int i, int v) {
push(w, L, R);
if (i <= L || i > R) return;
if (R - L == 1) {
st_cnt[w] += v;
} else {
int M = (L + R) / 2;
update_inc(w * 2 + 1, L, M, i, v);
update_inc(w * 2 + 2, M, R, i, v);
pull(w, L, R);
}
}
void force_lazy(int w, int L, int R) {
push(w, L, R);
if (R - L > 1) {
int M = (L + R) / 2;
force_lazy(w * 2 + 1, L, M);
force_lazy(w * 2 + 2, M, R);
}
}
struct Event {
int l, r;
bool start;
int id;
} events[200005];
int exterior[100005];
bool vis[100005];
int main() {
int T;
scanf("%d %d", &N, &T);
for (int i = 1; i <= N; i++) {
int X1, Y1, X2, Y2;
scanf("%d %d %d %d", &X1, &Y1, &X2, &Y2);
events[X1] = Event{Y1, Y2, true, i};
events[X2] = Event{Y1, Y2, false, i};
who[Y1] = i;
who[Y2] = i;
}
for (int i = 1; i <= N; i++) {
uf[i] = i;
}
int corners[2] = {0, 0}; // 0:exterior white, 1:exterior black
long long intersections = 0;
std::map<int, int> active;
for (int x = 1; x <= N * 2; x++) {
int l = events[x].l, r = events[x].r, id = events[x].id;
if (events[x].start) {
exterior[id] = query(l) % 2;
corners[query(l) % 2]++;
corners[query(r) % 2]++;
intersections += query(r) - query(l);
update_range_merge(0, 0, N * 2, l, r, id);
update(l, 1);
update(r, 1);
update_inc(0, 0, N * 2, l, 1);
update_inc(0, 0, N * 2, r, 1);
} else {
update(l, -1);
update(r, -1);
update_inc(0, 0, N * 2, l, -1);
update_inc(0, 0, N * 2, r, -1);
intersections += query(r) - query(l);
update_range_merge(0, 0, N * 2, l, r, id);
corners[query(l) % 2]++;
corners[query(r) % 2]++;
}
}
force_lazy(0, 0, N * 2);
int black_immersed = 0, white_immersed = 0; // cc surrounded by black/white
for (int x = 1; x <= N * 2; x++) {
int id = events[x].id;
if (events[x].start) {
if (!vis[find(id)]) {
if (exterior[id]) {
black_immersed++;
} else {
white_immersed++;
}
vis[find(id)] = true;
}
}
}
long long black_corners = corners[0] - corners[1] + intersections * 2;
long long white_corners = corners[1] - corners[0] + intersections * 2;
assert(black_corners % 4 == 0);
assert(white_corners % 4 == 0);
long long black_regions = black_corners / 4 + black_immersed;
long long white_regions = white_corners / 4 + white_immersed + 1;
if (T == 1) {
printf("%lld\n", white_regions + black_regions);
} else {
printf("%lld %lld\n", white_regions, black_regions);
}
}