Construct an undirected graph where each vertex represents a moo particle and there exists an edge between two moo particles if they can interact. An interaction corresponds to removing a vertex with at least one adjacent edge.
Within each connected component, at least one particle must remain. Conversely, we can show that this is always attainable. Consider a spanning forest of the graph; just keep removing a particle that is a leaf in this forest.
It remains to show how to compute the number of connected components in faster than O(N2). Sort the moo particles in increasing order of x and then y. Initially, suppose that each particle is its own connected component. Then while there exist two connected components that are adjacent in the order such that the minimum y-coordinate in the left component is at most the maximum y-coordinate of the right coordinate, combine them together.
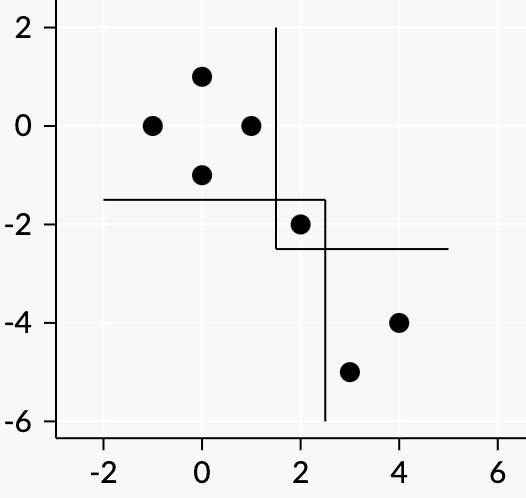
For the following input (a combination of the two samples), the answer is 3.
7 1 0 0 1 -1 0 0 -1 3 -5 4 -4 2 -2

After this is done, the i-th moo particle in the sorted order is not in the same connected component as the i+1-st if and only if min(y1,y2,…,yi)>max(yi+1,yi+2,…,yN) (which automatically implies that max(x1,x2,…,xi)<min(xi+1,xi+2,…,xN)). So after sorting we only need O(N) additional time to compute the answer.
Dhruv Rohatgi's code:
#include <iostream>
#include <algorithm>
using namespace std;
#define MAXN 100000
int N;
int x[MAXN], y[MAXN];
int cid[MAXN];
int minl[MAXN];
int maxr[MAXN];
bool cmp(int a,int b)
{
if(x[a]==x[b]) return y[a]<y[b];
return x[a]<x[b];
}
int main()
{
freopen("moop.in","r",stdin);
freopen("moop.out","w",stdout);
cin >> N;
for(int i=0;i<N;i++)
{
cin >> x[i] >> y[i];
cid[i] = i;
}
sort(cid,cid+N,cmp);
minl[0] = y[cid[0]];
for(int i=1;i<N;i++)
minl[i] = min(minl[i-1], y[cid[i]]);
maxr[N-1] = y[cid[N-1]];
for(int i=N-2;i>=0;i--)
maxr[i] = max(maxr[i+1], y[cid[i]]);
int ans = 1;
for(int i=0;i<N-1;i++)
if(minl[i] > maxr[i+1])
ans++;
cout << ans << '\n';
}
Related (but harder) problems: