This is probably the hardest bronze problem we've asked all season, befitting the fact that it's on the US Open contest (for which there is a longer time limit). It takes a good bit of thought to figure out the right solution structure, after which coding isn't too bad. I'll go through a couple of solution ideas in detail below. Hopefully you found this and the other bronze problems fun and challenging this season!
First, it may help to think of an instance where we cannot form a proper evolutionary tree. This would be an instance such that no matter how we form the tree, it would be inevitable that some characteristic would evolve in two distinct places in the tree. It turns out that the minimal such bad example looks like this:
population1: A population2: B population3: A B
In other words, we have a population with just trait A, a population with just trait B, and a population with both. If we want to build a tree out of this input, we would need to split on either A or B at the root, but then the remaining two subtrees would both need to have an edge that adds the other characteristic. For example, if the root split into "A" and "not A" branches, then both branches would need to contain an edge that adds the "B" trait.
It will help to actually look at things from the viewpoint of the characteristics instead of from the viewpoint of the populations, so let's "transpose" the input above:
A: population1 population3 B: population2 population3
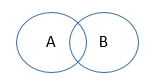
The fundamental problem here is that there are populations in A only, populations in B only, and populations in both A and B. If we look at the Venn diagram for the sets A and B, the picture therefore looks like this:

Let's call this situation a "crossing" pair of sets. In general, two sets can be disjoint (no overlap), nesting (one inside the other), or crossing (overlap but not nesting). If any two of the characteristics A and B in our instance represent crossing sets as above, then we cannot build a proper tree. On the other hand, if all the characteristics represent sets that don't cross (they are either disjoint or nested), then we get a Venn diagram like this:
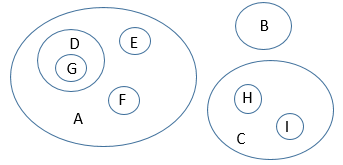
If you look at this picture carefully, hopefully you see a tree formed by the nesting structure of the sets:
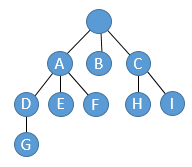
A tree like this is easy to convert into a proper evolutionary tree. E.g., if we have three children A, B, and C, we could just make three sequential two-way splits that add the A, B and C characteristics.
So, at the end of the day, we actually don't need to build a proper evolutionary tree, but we just need to test of any of our characteristics represent crossing sets; if so (and only if so), a proper tree is impossible to build. This leads to probably the easiest solution of the problem, shown in my code below where I build all the sets of populations having each characteristic and then just test if any pair of these sets is crossing.
Below this code, I'll discuss an alternate solution that also solves the problem and also builds the tree (if possible).
#include <iostream>
#include <fstream>
#include <vector>
using namespace std;
int N;
vector<string> characteristics[25];
vector<string> all_characteristics;
// Do two sets "cross" -- I.e., are there elements in A, B, and A intersect B?
bool crossing(int a, int b)
{
int A=0, B=0, AB=0;
for (int i=0; i<N; i++) {
vector<string> &v = characteristics[i];
bool has_a = false, has_b = false;
for (int j=0; j<v.size(); j++) {
if (v[j]==all_characteristics[a]) has_a = true;
if (v[j]==all_characteristics[b]) has_b = true;
}
if (has_a && has_b) AB++;
else if (has_a) A++;
else if (has_b) B++;
}
return AB>0 && A>0 && B>0;
}
int main(void)
{
ifstream fin ("evolution.in");
fin >> N;
string s;
for (int i=0; i<N; i++) {
int K;
fin >> K;
for (int j=0; j<K; j++) {
fin >> s;
characteristics[i].push_back(s);
bool found = false;
for (int k=0; k<all_characteristics.size(); k++)
if (all_characteristics[k] == s) found = true;
if (!found) all_characteristics.push_back(s);
}
}
int M = all_characteristics.size();
bool ok = true;
for (int a=0; a<M; a++)
for (int b=a+1; b<M; b++)
if (crossing(a, b)) ok = false;
ofstream fout ("evolution.out");
if (ok) fout << "yes\n";
else fout << "no\n";
return 0;
}
Another solution approach uses slightly different insight: suppose we have two traits A and B as follows:
A: (4 populations having trait A) B: (17 populations having trait B)
This means the "+A" edge in the tree (the edge adding trait A) cannot be an ancestor of the "+B" edge, since otherwise every population with the B trait would also have the A trait, contradicting the observation that the size of set A above is smaller than that of B. In general, this means splits on traits involving large sets of populations happen higher in the tree, and in particular the split at the root has to involve the trait with the largest sized set (the set having the most populations).
A method for building the tree therefore is to split on the largest trait, thereby dividing the populations into two groups, and then continuing to divide these groups the same way, always splitting on the largest available trait. If there is ever a tie for the largest trait (say, between traits A and B), some careful thought will convince you that either A or B would be suitable for the split at the root (this is clear if A and B are disjoint, and if A and B are crossing we will get into trouble later no matter what; A and B cannot be nesting if they have the same size). If we ever end up adding the same trait in two different places in the tree, we know that building a proper tree was not possible.
Here's a cool way to think about the approach above. Suppose we wanted to sort a bunch of 3-digit binary numbers. We could first sort them on their leading digit, giving a block of numbers starting with 0 followed by a block starting with 1:
010 000 011 --- 110 100 101
Then within each of these two blocks, we can do the same thing, sorting on the second digit. This makes our numbers sorted on their first two digits:
000 --- 011 010 --- 100 101 --- 110
Finally, sorting within each block on the last digit makes everything sorted.
If we write our different populations like this:
traitA traitB traitC traitD traitE... (in decreasing order of size)
population1 1 0 0 1 0
population2 0 1 1 0 1
population3 1 1 0 0 0
population4 0 1 1 0 1
.
.
.
Then each population is expressed as a binary number whose 1s and 0s reflect its traits. Now sorting these binary numbers the same way as above ends up basically running the tree construction approach we just described. We first sort on the leading digit, which separates the populations having trait A (the largest trait that we wanted to split on at the root) from those not having trait A. Then we split those groups on the second largest trait, and so on. So building the tree is much like sorting if we look at it from this perspective.
Note that this problem is directly applicable to real-world problems facing evolutionary biologists in terms of figuring out the most likely way organisms evolved in the past. The tree structure we are building is often called a "phylogenetic" tree in this area of study.